Simple 3D Scene (cont)

Please note that is the second part of the problem. Here is the first part.

The part of the scene as seen by player "through" the screen

Now as we can translate the real scene coordinates to user's frame of reference, we only need to create projections of the visible objects on our screen. As we remember, the imaginary screen is a glass rectangle through which the user looks into virtual world. We want its aspect ratio be the same as real user's screen has (i.e. the monitor) - then we'll be able to easily translate screen coordinates between imaginary and real.

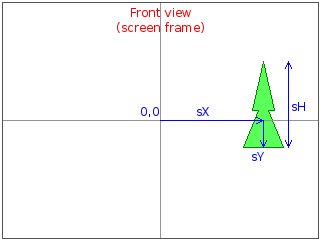
What are these screen coordinates? Let us assume that imaginary screen has the origin in its center, like in the picture above. We agreed to represent (mathematically) all objects as having two coordinates X and Y and some height H.

After translation of coordinates the objects with Y=0 are directly in front of us and should be drawn in the center of the screen. Greater X places the object further from us, so its projection decreases in size. Positive values of Y shift the projection on the screen to the left and negative values to the right.

Let us call screen coordinates sX, sY and sH as shown in the picture. Of them sX is the horisontal position of the projection (which itself is vertical line). The lowest point - one where projection touches "imaginary ground" is sY (at the picture it is negative). Protection raises from (sX,sY) by the height of sH.

We are going to calculate them one by one. At first let us take care of sX:

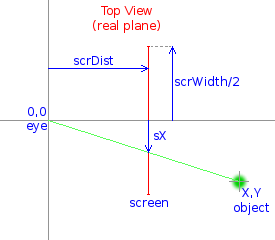
Here we see the part of the scene from the above, with X-axis of the scene piercing the center of the screen, which is placed orthogonally to it at the distance scrDist from the eye of the player - i.e. the middle of the screen is at point (scrDist, 0), while edges are at (scrDist, +/- scrWidth/2).

It is quite intuitive that sX is governed by simple ratio. It is as many times smaller than Y (by absolute value) as many times scrDist is smaller than X, so we can write (note that sX and Y have opposite directions):

sX = -Y * (scrDist/X)

Yes, it was that simple! Now how to calculate sY and sH? Let us see another picture, view from the side. We assume that player's eye is at some height above the ground, while all objects have its lowest point on the ground:

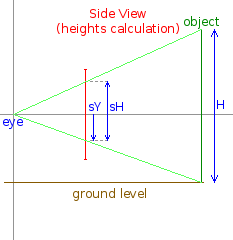
The picture feels similar! We see that there are the same proportions:

• sY is as many times smaller compared to the height of the eye above the ground (let us call it eY) as scrDist is smaller than X;
• sH is as many times smaller than the height of the object (H in picture) as srcDist is smaller than X.

Let us write all three formulas then (introducing common coefficient K):

K = scrDist/X

sX = -Y * K
sY = -eY * K
sH = H * K

The only thing remaining is to convert these values into coordinates of the real screen. I.e. while our imaginary screen is a rectangle with dimensions scrWidth and scrHeight and origin in the center, real screen instead is W by H pixels and have origin in the upper-left corner (so that vertical axis is usually inverted).

Problem Statement

Your goal would be to calculate these values for several objects and translate them into real screen coordinates. We assume the following constant values:

• real screen has size of W=480 by H=360 pixels;
• imaginary screen is placed at distance scrDist=0.5 from the user and have width of scrWidth=0.4 (and height of scrHeight=0.3 to conform with real screen's aspect ratio);
• the height of the eye above surface is eY=1.0.

Input data will contain the number of the objects in the first line.
Next lines will have X, Y and H - coordinates (after translation to player's frame of reference) and the height for each object.
Answer should give coordinates of projection on the real screen - one horizontal and two vertical (lower and upper), we can call them rX, rY1 and rY2 for example (rY1 > rY2). Of course these values should be rounded to integers (since we usually do not work with fractions of pixels).

Example:

input data:
2
4 0 2
7 2 3

answer:
240 330 30 69 266 9