Simple 3D Scene

Please note - this problem is split into two tasks to make explanation and debugging less complicated. Here is the second part.

Nowadays 3-dimensional games are very usual. However at the 1990-s they looked like some fantastic from the future - notwithstanding that image and scene quality was far lower. Wolfenstein and Doom were met with great enthusiasm among gamers - while puzzling programmers with question "How could this be done?"

Let us learn the rendering of basic 3D scene. Games with such graphics were preceding two mentioned above - they could be met even on platforms like ZX-Spectrum. Instead of putting user into some whimsical maze of rooms they gave you an image of open and almost plain space. You should be able to play with the demo above to get the feeling of such games.

Though simple, it allowed wide range of game ideas - from rallying through the forest to hunting enemy tanks etc. This approach allows rendering simple sprites (images like these fir-trees) and opaque shapes like pyramids (hills and mountains) or cubes (buildings etc.) - though often without any texture.

Let us concentrate on rendering sprites - you will easily invent any other tricks if you understand necessary calculations.

Assume for simplicity that the sprite is a vertical segment of the line, sticking upwards from the ground. (When you are ready to draw images instead of lines, they only need to be scaled to the same height and placed so that the line passes through their center). So the sprite on the plane is determined by its coordinates (X, Y) and its height.

The player also is at any moment placed somewhere - his position is described not only by two coordinates, but also by direction in which he is looking. The first step to render the scene is to translate coordinates to player's frame of reference. This operation is just an extention of Rotation in 2D Space problem.

Coordinate translations

Look at the scene through the prism of math (as seen from above). Green dots are objects surrounding the player (like trees). The player himself is small blue dot - and blue arrow shows the direction which he is looking at.

Imagine that the player holds before him transparent glass screen, through which he is observing the scene. This screen is shown as a red segment in a picture. Surely it is not possible for player to see objects which fall outside the bounds of this screen. So the visible part of the scene is an angular sector (outlined with grey).

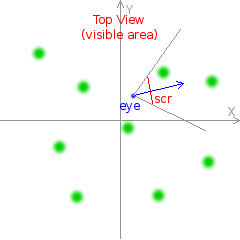
Before rendering anything on the screen it is quite convenient to translate the coordinate system in two steps:

• move it so that origin is placed in the same point with player;
• rotate it so that player's sight is directed along X axis.

Below is the same image, but with coordinate system translated to user's:

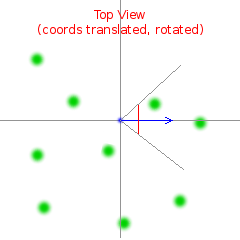
Problem statement

As a first part of scene rendering, you are to perform coordinates translation and rotation and then output new coordinates of objects, but only of visible ones. Besides limiting visible area by angle let us also agree that it is limited by range - i.e. objects very far away are not visible (which is convenient if the scene is very large).

Constant parameters:

• scene is square with sides of 100 units;
• objects are placed here randomly so they coordinates are -50 <= X,Y <= 50;
• distance from player to his screen (in virtual world) is 0.5 units and width of the screen is 0.4 units;
• objects are visible if they are no closer to the user than the screen itself (0.5) and not further than 60 units away.

Input data contains total amount N of objects (points) in the first line.
The second line contains coordinates of the player pX, pY and pA (angle in radians, counterclockwise from the X-axis direction).
Then N lines follow giving Xi and Yi for i-th object.
Answer should contain coordinates of the objects after translation, in the same order as given in input, but skipping those out of visibility. Values should have precision 1e-7 or better.

Example:

input data:
3
1 1 0.78540
40 -2
11 11
-8 -3

answer:
14.142135624 0

After we have all coordinates translated, we need only sort objects by decreasing of distance to them (so we can drow the furthest at furst and they will not overlay nearer ones) - and then draw images of these objects on the screen calculating screen coordinates as explained in the sequel to this task.