Calculation of Pi

From ancient times we know of the number Pi - it shows how many times longer is circumference of the circle compared to the diameter.

We know it has endless and non-repetitive pattern of digits when represented as a decimal. It starts with: 3.14159265358...

Curious question is - how did people calculated its numerical value at all? Obvious idea is that some ancient greek may use a rope to measure the circumference of some round column. However this is hardly sufficient even for two digits after decimal point because any rope is slightly elastic and any column is slightly imperfect.

Instead some pure-mathematical approach should be used. Probably one of the first was proposed by Archimedes more than 2000 years ago.

The idea is simple:

• let us use perfect hexagon as a first approximation of a circle;
• hexagon has its sides equal to the radius of the circle drawn around it (and touching its vertices) - so its perimeter is 6*R;
• now let us convert hexagon to dodecagon with 12 sides - splitting each of the hexagon's sides in two;
• using some geometry consideration (described below) we can find the length of the side of the shape with doubled amount of sides - and so find its perimeter as a better approximation for circle's circumference;
• now we can proceed splitting sides and approximating circle with perfect polygon of 24, 48, 96 sides and so on.

Surely polygons with that many sides are already quite close to circle so approximation converges fast enough.

Splitting sides

Now, how can we convert polygon of N sides to another with 2*N sides? I.e., how should we calculate the length of a side of new polygon?

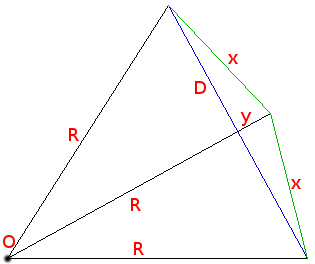
Regard the picture above. Point O is the center of the circle and blue line of the length D is one side of original polygon (say, hexagon). There are two radiuses of the length R drawn from the center to the ends of this side.

Now if we want to split this side D exactly in two, we draw the third radius R (one in the middle) to be orthogonal to this side. Then we draw two new sides of the yet unknown length x (green lines) to this new radius.

Note that middle radius R is split in two (unequal) parts by crossing the side D. Let us mark the shortest of these two parts as y and the rest as h=R-y. Of course we do not know length of any of them still.

Also let us use letter d for the half of the side D, i.e. d = D/2.

See, here are several right triangles at the picture!
One is formed by outer radius R, half-side d and the part of the middle radius h.
Another, smaller, consists of the d, y and x.

For both of these triangles Pythagorean Theorem holds, so we can write:

R^2 = d^2 + h^2     =>      h = sqrt(R^2 - d^2)

x^2 = d^2 + y^2     =>      x = sqrt(d^2 + (R-h)^2)

So we can easily calculate the length of the new side x - and use this method for approximating the circle with polygons!

Integer calculations

Since we want to know many digits of Pi we could not use imprecise floating-point types.

Instead we will choose R to be very large integer, like 1 000 000 000 000 000 000 = 1e18 and then we can perform all necessary operations on integers. Let us agree that:

• whenever we divide integer by integer (usually it would be division by 2) we throw away fractional part, simply rounding the result down;
• and if calculating square root of some Z (with Heron's method for example), we should use as a result the greatest integer M such that when squared it does not exceed Z (i.e. M*M <= Z).

So for example with radius R = 1e18 and starting with hexagon with D = R we calculate:

d=500000000000000000  h=866025403784438646  side=517638090205041524  (for 12 sides)
d=258819045102520762  h=965925826289068286  side=261052384440103182  (for 24 sides)
d=130526192220051591  h=991444861373810411  side=130806258460286133  (for 48 sides)
d=65403129230143066   h=997858923238603506  side=65438165643552283   (for 96 sides)

And to get the value of Pi (well, without decimal point) we need to multiply side by amount of sides and then divide by 2 (that is why it is good to use R equal to some power of 10):

Pi = 96 * 65438165643552283 / 2 = 3141031950890509584

Of course if we repeat this algorithm too many time, side may decrease to very small values so the precision will be lost.

Problem statement

Input data will contain value K between 100 and 200 which you will use to set radius as R = 10^K.
Another value N will be given - how many steps of algorithm to perform (so the last polygon has 6 * 2^N sides).
Answer should give the representation of Pi (without decimal point) after that many steps.

Example:

input data:
37 11

answer:
31415926193653839551895493120653182976

Note: since this exercise requires long-arithmetic, it is better to user language which have built-in types for this, like Python or Java.