Gradient Calculation

Gradient is the same thing as derivative, but applied to function with more than one parameter. Physical meaning is just the characteristic of the slope at the given point (though it is hard to imagine for functions with 3 or more arguments) - its direction and steepness.

For example suppose we have a 2D function like the following:

f = f(x, y) = x * x + y * y

And we want to find the gradient value at point (1, 2). Let us calculate the value of the function at this point and then at two neighboring points with offset of dt = 0.1:

f(x0, y0)      = f(1.0, 2.0) = 1.0 * 1.0 + 2.0 * 2.0 = 5

f(x0 + dt, y0) = f(1.1, 2.0) = 1.1 * 1.1 + 2.0 * 2.0 = 5.21

f(x0, y0 + dt) = f(1.0, 2.1) = 1.0 * 1.0 + 2.1 * 2.1 = 5.41

The gradient is a vector of values, representing the tangent of the slope in each direction (by x and by y in our case):

g(x0, y0) = [(f(x0 + dt, y0) - f(x0, y0)) / dt, (f(x0, y0 + dt) - f(x0, y0) / dt] =
          = [(5.21 - 5.00) / 0.1, (5.41 - 5.00) / 0.1] =
          = [2.1, 4.1]

Of course this way of calculations will give precise value for gradient only when dt is infinitesimal (i.e. "non-measurably small" or "infinitely small") - though for practical reasons we can use some finitely small values, like 1e-9 and calculate gradient with given precision.

Slope direction

The direction of the resulting vector, i.e. in our case:

atan2(4.1, 2.1) = 63 degrees from axis X, counterclockwise

is the direction in which the slope at this point raises most steeply. At the same time the reverse direction is the one of the fastest descent from this point. This still works for functions with more than two arguments, i.e. for spaces with more dimensions - though it is hard to imagine visually.

We now are going to practice calculation of gradient with a small program - this is important for some further tasks (i.e. ones about searching for minimums with fastest descent path etc).

Problem statement

You are given a function in the form (with A, B and C being some constants):

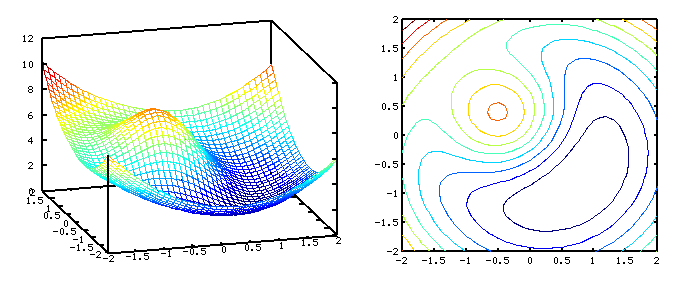
f = f(x, y) = (x - A)^2 + (y - B)^2 + C * exp(- (x + A)^2 - (y + B)^2)

It looks like a wide bowl having small peak somewhere inside, see the pictures above.

You will be given some points, as pairs of coordinates (x, y) and asked about the direction of the descent from this point.

Input data will contain four values in the first line: N - the number of points, then constants A, B and C.
Next lines will contain one point each, as a pair of cooridnates X and Y.
Answer should give integers in range from 0 to 360 - the direction of the descent of the slope in each of the points, expressed in degrees and rounded to whole integers.

Example:

input data:
14 -0.5 -0.4 7
0.3 0.2
0.4 -0.5
-0.7 0.1
-0.7 -0.7
0.3 0
0.6 -0.5
-1 -0.7
-0.8 0.8
-0.2 0.9
0.1 -0.4
0.4 -0.6
0.6 -0.5
-0.2 0.8
-0.8 0.2

answer:
222 246 211 212 234 254 19 214 172 234 244 254 175 213

Note you will do wise if you'll try to calculate a grid of points of the function and plot its mesh 3D view or better its contour representation with the tools like Excel or Matlab / Octave to see whether your answers give proper directions. See the pictures at the top of the page as an example of these plots.