Breadth First Search

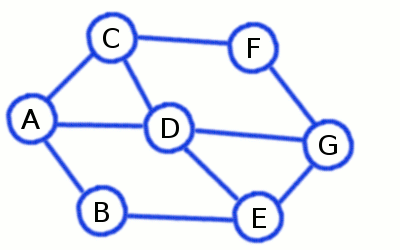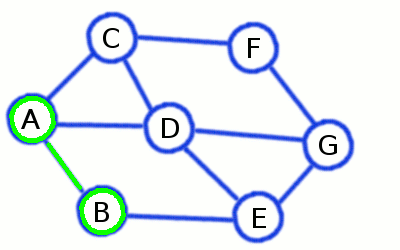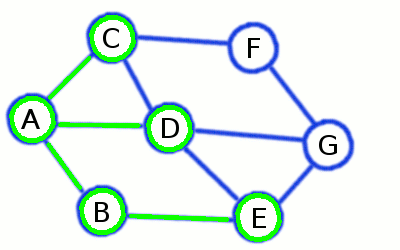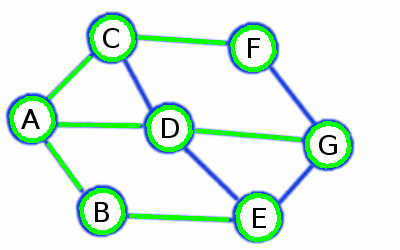
Breadth-First Search builds a short and divergent spanning tree

Breadth-First Search with its complement Depth-First Search are two popular methods of searching in the graph. They are building blocks for many other more special algorithms. At the same time each of them may be implemented in several different ways.

The words Breadth-First in the name reflect the manner of search - from any vertex we are trying to investigate all neighbors as soon as possible. Because of this the search process looks as following:

• at first we visit the initial node itself - let us call it level 0;
• then we visit all nodes immediately reachable from the initial node - let us call them level 1;
• on the next step we reach all nodes immediately reachable from level 1 and call them level 2.

And so on with the general rule that at level K+1 we visit all neighbors of all nodes of level K, of course except ones already visited on previous steps. At the picture above initial node is A, while the first level consists of B, C, and D - and the second contains remaining E, F and G.

The manner in which the algorithm visits vertices resembles the spreading of the wave when it floods the shore. Due to this fact particular implementation of the BFS on a rectangular grid is sometimes called Wave Algorithm - see the following picture to decide whether this name is correct:

Wave algorithm is just another incarnation of the BFS

Typical application

If the graph is connected, BFS will visit all of its nodes. If for each node we will remember where we got to it from - then the resulting set of edges will represent a tree connecting all nodes (so-called spanning tree).

The tree built by BFS at the same time represents the shortests paths from initial vertex to any other (for the graph with the edges of equal weights - otherwise more special algorithm, like Dijkstra should be used).

The puzzle Word Ladders gives an example of a problem when BFS is most suitable.

Other popular usage is for discovering if the graph is connected or consists of several izolated parts. It also allows to mark which vertex belongs to which part. However this task could be by DFS also.

Algorithm implementation

Usually we prefer to use a Queue to keep the track of the nodes which we are going to visit soon. This data structure provides two operations, let us call them add and remove for putting new elements to it and fetching them later. The core property is that elements are removed in the same order in which they were stored - this is often called FIFO, i.e. first in, first out. For example if you add elements to the end of the list and remove them from the beginning - it will work as a queue.

We also need some way to mark vertices as seen - it could be array of flags or set to which we will add ids of vertices or something like this.

That's how algorithm works:

1. We add the initial node to queue and mark it as seen.
2. Remove the next element from the queue and call it current.
3. Get all neighbors of the current node which are not yet marked as seen.
4. Store all these neighbors into the queue and mark them all as seen.
5. Repeat from the step 2 until the queue becomes empty.

Usually we perform some additional actions along with these core steps. For example:

• after fetching each vertex from the queue we may print its name out - this will give us a list of the vertices of the graph (or its connected component) in the order of visiting by BFS;
• if using hashtable (aka dictionary) or array for seen we can store here not only the fact that the node was seen, but also the id of the vertex from which it was seen - as the result the hashtable will describe the tree of the shortest paths at the end;
• distance to the given vertex from the initial one could be stored in a separate array or hashtable.

You also can read wikipedia article to get more clear idea.

Problem statement

You are given an undirected and unweighted graph with vertices identifided by integers. The goal is to run BFS over it as described above, starting from the node 0.

As output you should produce the seen array which shows where each vertex was visited from.

To avoid ambiguosity please at the step 3 sort all fetched neighbors in order of increasing their id numbers.

Input data will contain the amount of nodes N and the amount of edges M.
Then M lines will follow each containing ids of two nodes connected by an edge. Node ids are integers between 0 and N-1.
Answer should contain the seen array as described above. It should have -1 for the initial node.

Example:

input data:
7 10
0 1
2 0
0 3
1 4
4 3
2 3
5 2
6 3
4 6
6 5

answer:
-1 0 0 0 1 2 3

This example is from the picture above, only vertices are labeled with 0...6 instead of A...F.