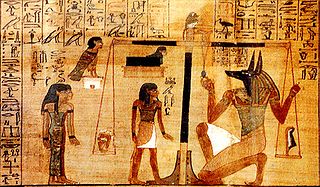
Beam Balance is a device for measuring unknown weights by balancing them with a set of known masses. As you may see from the picture above, they were known even in Ancient Egypt more than 3000 years ago.
The device consists of the horizontal beam holding two pans. The object to be measured is placed at one pan and some masses of known weights are collected upon another until the beam will return to horizontal position showing that weights on both pans become equal.
In the case above the object is the heart of a man and the feather of truth is used as a mass. At this scene participants are not interested in the exact weight of the heart but rather try to check whether it is lighter or heavier in comparison to some standard.
Set of Masses
Most of sets of masses provide standards of the weight based on decimal system, for example:
1g 1g 2g 5g 10g 10g 20g 50g
These eight masses allow us to represent any weight up to 99 grams. Of course you may say that if we use binary
system, less masses are needed:
1g 2g 4g 8g 16g 32g 64g
Here are only 7 instead of 8 and they allow to represent weights up to 127 grams! Can we reduce the number of
masses further?
Yes, we can! Because we can place some smaller masses onto the pan with the weighed object, effectively subtracting their weight from other masses. Regard the following set of masses:
1g 3g 9g 27g 81g
Suppose the weight to measure equals to 55g. Then we place masses of 81g and 1g onto the free pan and 27g onto
the pan with the object:
object + 27g == 81g + 1g
So you see, only 5 masses allow to measure weights upto 121 gram.
Problem statement
Given some weight you are to tell how many masses from this last set should be used to represent it.
E.g. 55g is represented with 3 masses in example above.
You may use any mass equal to some power of 3 (i.e. not limited with 81 but further with 243, 729 and so on) -
though none could be used more than once.
Input data will give a number of test-cases in the first line.
Next line will contain test-cases - each with a single value - the weight to represent - not exceeding 2 000 000 000 grams.
Answer should contain the amount of masses used for each weight.
Example:
input data:
17
5 10 15 20 25 30 35 40 45 50 55 60 65 70 75 80 85
answer:
3 2 3 4 3 2 3 4 3 4 3 4 5 4 3 2 3
Let us see how few first weights of this example are represented:
5 == 9 - 3 - 1
10 == 9 + 1
15 == 27 - 9 - 3
20 == 27 - 9 + 3 - 1