The following fragment is from Jacob Perelman's book "Geometry can be fun":
"When I was a child, I once had seen the forestry master measuring the height of trees. This old man aimed at the top of the giant pine with some small wooden device - and I expected he would immediately start climbing there with measurement chain - but he instead told that measurement is already done! Funny - I did not realize it was ever started..."
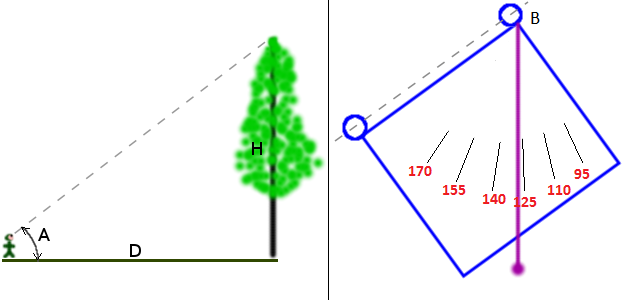
The problem of measuring the inaccessible height is a great way to introduce basics of trigonometry. Look at the picture
on the left. Here we see the forestry specialist looking at the tree which should be measured. This person does not
know the height H of the tree, but he can measure (even by walking) the distance to the trunk D and also (with some
convenient tool) the angle A between horizontal line and the line of sight aimed at the top.
Line of sight together with D and H forms the right triangle. That means we can freely operate with sine,
cosine and tangent of the angle A. Of them the tangent is the most suitable because:
The tangent of a given angle (in the right triangle) is the ratio of the opposite and adjacent sides.
In our case the side opposite to the angle A is H and the adjacent one is D so:
tan(A) = H / D
Tangent of the angle is not a simple function and hence is usually calculated either by special table, or with calculator (computer) and, well, some people can simply remember its values.
In this equation we therefore know tan(A) and D, so we can calculate the height H:
H = D * tan(A)
You may read more in wikipedia on trigonometric functions.
Angle measurement tool
The right picture shows small handheld tool which helps measuring the angle A. It is simple square piece of wood
(outlined in blue) with two sights attached to the upper edge so it could be aimed to the top of the tree. Here line of
view is depicted as grey dashed line, passing through two round sights.
There is also small plumb (like pendullum) attached, which will always hang vertically down (it is shown in violet). The higher the tool is aimed, the more is declination of the plumb - a small scale is drawn on the face of the tool (short black lines).
So after aiming the device to the tree top, we should notice the label on the scale at which the plumb stops - and read
the corresponding angle. For example the scale can have marks from 90 to 180 degrees meaning the angle between the
line of sight and the line of the plumb (vertical down). Alternatively scale could be graduated in tangents already to
simplify calculations or something like this.
Problem statement
Now we are to help the old forestry master to measure heights of several trees. For each tree you are told the distance
D to it and also the angle B between the line of sight (to the top) and the vertical line given by plumb. So the
angle B is 90 degrees when line of sight is horizontal and is 120 degrees when the line of sight is raised 30
degrees above horizont - it is up to you to guess how A should be calculated from B :)
Input data will contain the amount of the trees we want to measure in the first line.
Next lines will contain a pair of values D and B each (one line for each tree), angle is specified in degrees.
Answer should contain the heights of the trees in the same order, rounded to nearest integer.
Example:
input data:
3
71 134.182
47 139.994
121 109.983
answer:
69 56 44
This exercise is, probably, too easy, so you are encouraged to proceed to Cloud Altitude Measurement!