Page Rank as Eigenvector

This problem is inspired by the first week of Mining Massive Datasets course at Coursera.

After you have solved Page Rank you may wander that random walker experiment may have some strict mathematical form. And really it has.

Suppose we have a single walker who is randomly placed into one of the nodes. Then he performs many-many random steps and we are curious about probability that he ends in a certain node.

For example, if there are only two nodes, then the walker have probability 1/2 = 0.5 to appear in any of them at a certain step.

We can represent a graph as a matrix where element (i,j) contains non-zero if there is walker can get to i-th page from j-th by the link. And this non-zero value describes the probability that the walker will choose the given link to leave the j-th node. For example look at the following graph:

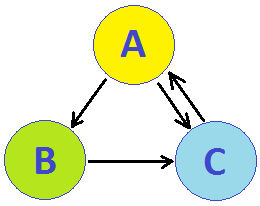
Here the walker can leave B and C node by only one link, so that edges B->C and C->A both give entries of 1.0. However, there are two outgoing links from A and so they (A->B and A->C) give values of 0.5 only. Here is the matrix:

  |  A   B   C
--+-------------
A | 0.0 0.0 1.0
B | 0.5 0.0 0.0
C | 0.5 1.0 0.0

You see, this transition matrix have the sum of each column equal to 1 - the total probability of leaving the node.

Now suppose we have found the page rank for each node as a vector of probabilities that walker appears at these nodes after many steps:

    | pA |
r = | pB |
    | pC |

Such vector will satisfy an interesting matrix equation:

r = M * r

where M is the transition matrix. Really the product of matrix and vector is another vector, where each k-th element is determined as product of k-th row of a matrix by the initial vector. To multiply a row by a vector we simply sum the products of their corresponding elements (first-by-first, second-by-second etc.)

This means that first element of resulting vector is the sum:

M(1,1) * pA  +  M(1,2) * pB  + M(1,3) * pC

but M(i,j) describes the probability of transition from j-th to i-th vertex! So when we multiply these probabilities by the probabilities that the walker already was at given nodes - and sum them - we get the total probability that on the next step he gets to the i-th node. Of course these probabilities should be the same as given by vector r!

Eigenvector

But this equation is just a special case of an eigenvector and eigenvalue description! Really, in general case we write:

a * r  = M * r

where a is an eigenvalue and r is the corresponding eigenvector of a given matrix M. In our case it is just the same with a=1.

This is very nice since it means we can use some popular method of calculating eigenvectors to find page rank. Very popular (and very simple) is the Power Iteration method:

• simply initialize r to some values, for example 1/N where (N is the number of nodes and the length of the vector);
• then perform multiplication M*r several times, taking the result as new approximation of r.

When difference between next and previous values of r becomes negligible - we can be sure r is an eighenvector.

Dead Ends and teleportation

There is a small problem to take care of. Suppose we have a graph containing two parts such that one is reachable from other but there is no way back. Simplest case is the graph of two nodex X and Y with a single edge from X to Y.

Obviously any amount of random walkers will get trapped in such a dead end part and it will look like the page rank of Y document is infinite times greater than that of X.

For larger example see the picture at the previous problem - if walker will leave red nodes he will never be able to return to them.

To compensate such an issue, we introduce random teleporting. I.e. we agree that for each step the random walker have probability beta to proceed by any of the outgoing urls, but also with small probability (1-beta) he can jump to any of the pages (chosen at random).

To amend the matrix equation above we only need small modification of M:

• create matrix Z of the same size as M, filled with values of 1/N (teleportation matrix);
• multiply M by beta;
• multiply Z by (1-beta);
• sum them both to get new MZ matrix.

The equation remains the same:

r = MZ * r

Problem statement

Now you are to apply these knowledge to calculate page rank more precisely. You are given a small web-graph in a same manner as for previous problem and you should output page ranks calculated with beta=0.8 (i.e. probability of teleportation is 0.2). Note that eigenvector (and pagerank) could be scaled (multiplied) by any value and equations will remain correct.

Please, scale them so their sum is 100 in total (i.e. they will give probabilities of appearing at given page expressed in percents).

Input data contains number N of nodes (pages) in a graph - and then number M of edges (hyperlinks between pages).
Next M lines describe one direct edge each by two values - index of the source and target node (indices are in range 0..N-1).
Answer should contain N values - each meaning the probability of the random walker appearing at given node after very many steps (and teleportations), expressed in percents (tolerance about 0.1% should be OK).

Example:

input data:
10 18
0 3
0 4
0 5
1 0
1 6
2 1
2 9
3 4
4 0
4 7
5 3
6 9
7 2
7 8
8 2
8 6
8 9
9 2

answer:
10.59 9.71 19.25 8.68 11.77 4.82 7.13 6.71 4.68 16.66