Maximum Flow - CodeAbbey

This is a quite popular problem on graphs: having some network (e.g. of pipes) in which all connections (edges) are of known capacity (maximum possible current) we are curious to know what is the maximum possible flow between two chosen nodes source and destination.

Such algorithm could be applied to water pipes, or computer networks, or nets of automobile roads - and also to several less visibly related optimization tasks - among them is the problem of Optimal Marriage (hope we'll discuss it further).

In this exercise you will be given a graph and asked to find maximum flow between two of its nodes. There are many possible approaches and if you know any - then skip to Problem Statement section. Otherwise let us study simple but yet effective algorithm.

Ford-Fulkerson Algorithm

This approach works for cases with integer capacities of edges and looks as following:

For each edge we define not only its max capacity, but also its current flow, which is initially 0 for all of them.
Now find any path from source to destination in which every edge has currently flow less than capacity (so that it can bear some more).
For this path calculate additional flow which we can send via this path - i.e. iterating over every edge of the path, determine narrowest among them - that which has minimum of capacity - flow.
Increase flow along each of these edges by the value we calculated in previous step.
Repeat from step 2 until no more path could be found.

The path could be searched for with any suitable algorithm, e.g. Breadth-First-Search.

Let us see an example with pictures. Here is a graph with 4 nodes and 5 edges. We want to calculate maximum flow between A and D. Note that blue values are capacities of edges while red ones mean existing flow in the given edge before we find new path through it.

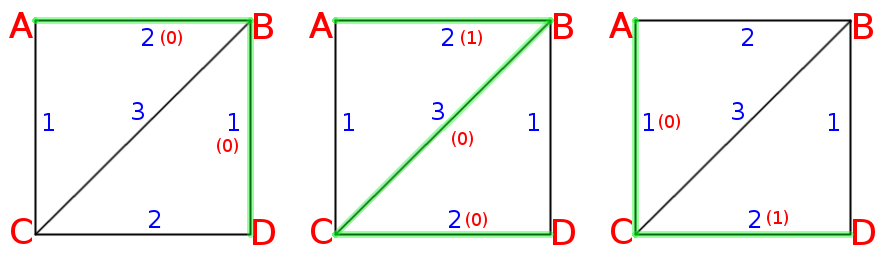
On the first iteration we find a path A-B-D, which consists of edges with capacity 2 and 1. So we can send a flow of 1 along this path.

Next we find a path A-B-C-D which consists of edges with capacities 2, 3 and 2. However the first edge already have flow of 1 in the same direction, so that additional flow is only 1. We send it along these three edges (so taht edge AB is now "saturated").

The third path is A-C-D and consists of edges with capacities 1 and 2. The latter already have a flow of 1 but anyway we can send flow of another 1 along this path. Now the edge AC is "saturated" too and we obviously could not improve any further.

So the resultant max flow is 3. Let us see how this looks with adjacency matrices representing our graph.

adjacency matrix            flow matrix

  |  A  B  C  D               |  A  B  C  D 
--+-------------            --+-------------
A |  *  2  1  *             A |  *  0  0  *
B |  2  *  3  1             B |  0  *  0  0
C |  1  3  *  2             C |  0  0  *  0
D |  *  1  2  *             D |  *  0  0  *

As you see, we also initialize second matrix to register flows over edges in it. After the first iteration the flow over A-B-D is added:

  |  A  B  C  D 
--+-------------
A |  *  1  0  *
B | -1  *  0  1
C |  0  0  *  0
D |  * -1  0  *

Note that we also mark negative flow for the same edges in backward direction. This makes sense because at some point we can find a path which will require reverting flow at some intermediate edge (and we'll find that with capacity for example 3 it has flow -1 in given direction - so that flow up to 4 could be "added").

Now let us proceed with two next steps:

add path A-B-C-D            add path A-C-D

  |  A  B  C  D               |  A  B  C  D 
--+-------------            --+-------------
A |  *  2  0  *             A |  *  2  1  *
B | -2  *  1  1             B | -2  *  1  1
C |  0 -1  *  1             C | -1 -1  *  2
D |  * -1 -1  *             D |  * -1 -2  *

We may note a couple of important properties:

for each intermediate node the sum flow (incoming + outcoming with respect of sign) is always zero (do you remember 1-st Kirchgoff Law?);
for source and sink the sum is max_flow and -max_flow respectively.

These are pretty evident - surely the water in the pipes could not mysteriously appear and disappear.

Problem Statement

Input data will tell you in the first lines N, M, S, D - amount of nodes, of edges, source node and destination node.
Then M lines will follow with three values each A, B and C meaning that edges A and B are connected with an edge of capacity C - all edges are regarded as bidirectional.
Answer should have a single value - maximum flow.

Example:

input data:
4 5 0 3
0 1 2
0 2 1
1 2 3
1 3 1
2 3 2

answer:
3

Another Important Example:

input data:
8 9 0 3
0 1 1
0 4 4
1 2 2
1 6 4
2 3 1
2 5 4
3 7 4
4 5 4
6 7 4

answer:
4