Chords of Music

Note names on piano keyboard. Notes with shaprs also have alternative names with flats here.

We are going to learn bit more about music.

You probably know that music may sound either joyfully and lightly, or seiously, melancholic or even sad.

This "temper" of the music is based on very simple math relations! Prepare for this great mystery to be unveiled! :)

From the Pitch and Notes you may have learned few things important for this task:

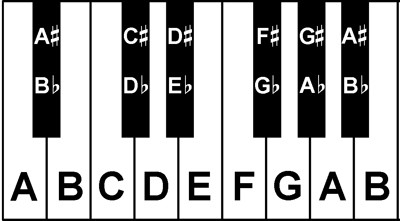
• that musical notes follow in equal steps (semi-tones) on logarithmic scale of sound frequency;
• that 12 steps make full octave, after which notes repeat but with doubled frequency;
• that notes have 12 names to distinguish them in the scope of octave (and octaves have their names or numbers also).

Here are the note names again, placed in order with one semitone step between them:

C  C#  D  D#  E  F  F#  G  G#  A  A#  B

There is an important concept of chord - the union of several notes played either simultaneously or close one after another. We will only discuss two main chords - major and minor.

Both of these chords consist of three notes of different pitch. They are called root, third and fifth. In the pure form of the chord the root has the lowest pitch and the fifth has the highest.

And even more, they have precise amount of steps between them:

• fifth has pitch 7 steps (semi-tones) higher than root;
• third is either 3 or 4 steps higher than root;
• if third is 4 steps higher than root then it is major chord;
• and in minor chord third is only 3 steps higher than the root.

So if we want to build the major chord with note D as a root (e.g. D-major) we need to play D, then F# (which is 4 steps from D) and at last A (which is 3 steps from F# and 7 from D).

The table below shows the notes of D-major and D-minor chords so you can count the steps yourself.

          | C  C#  D  D#  E  F  F#  G  G#  A  A#  B
      ----+-------------------------------------------
D-major   |        *      4     *     3    *
          |
D-minor   |        *    3    *      4      *

Of course if while building a chord we met the end of octave, we simply wrap to the next octave, e.g. for A-minor the notes would be A, C and E.

Great Mystery

And now here is the secret - major chords make "happy" and "joyful" sound, while minor chords bear melancholic and even mournful expression. You may found sample sounds in the wikipedia page about 3-note chords.

Now another curious thing - any note of the chord could be shifted by the whole octave (or several) up or down - the chord will retain its temper. E.g. raising or lowering any note by k*12 steps does not break the chord!

Popular example of this is an Inverted chord where, for example, the root is raised one octave up. Sometimes they are distinguished from pure chords, but generally speaking they could substitute one another for example if it is easier to play without breaking fingers.

Another example is playing additional sound to the chord - the same as root but lowered octave or two - such a base bass note which may be useful to audibly highlight accents while accompanying vocal etc.

Problem statement

You are given several notes described by their numbers according to MIDI-standard - C of the 0-th octave is 0, D in the same octave is 2, B is 11 and so on, so that 64 means E of the 5-th octave.

The task is to determine what chord these notes represent.

Input data contain the number of test-cases in the first line.
Next lines contain from 3 or more integers - numbers of notes played.
Answer should contain respective chord names in form C-minor, F#-major or the word other in cases when notes do not form one of these two chords at all.

Example:

input data:
3
87 73 64 61
46 37 53 58 70
44 48 51 56 32

answer:
other A#-minor G#-major